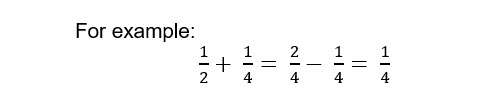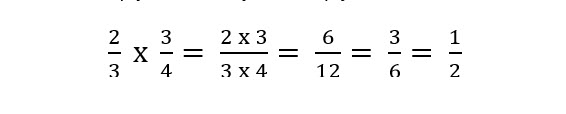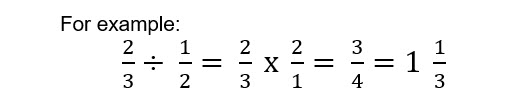Working with whole numbers and fractions

Note: These lessons are excerpted from Luther Maddy’s Workbooks (C) 2024

Watch the Videos

Reviewing Whole Numbers & Fractions

Using coins to better understand fractions Using coins to better understand adding and subtracting fractions

Whole numbers defined

A whole number is a complete number. Whole numbers are the numbers you first learned. They are the numbers on the number line, i.e. 1, 2, 3, 4 etc. you used in grade school. We sometimes call whole numbers integers. Whole numbers or integers will have no fraction or decimal value associated with the number.

Our numbering system is the decimal system. The prefix “deci” mean “10”. Everything in our numbering system is based on 10’s. For instance, there are 10 digits, 0 through 9. And, when a number has more than one digit, each subsequent column represents an increase in terms of 10 times the column to the right.

When writing whole numbers, we use commas (,) to separate each group of three digits, i.e. 10,000 or 1,000,000.

Fractions

Fractions represent a point between zero and one on the number line.

A mixed number is a whole number and a fraction, 1 ½. Fractions have a numerator, the number on the top and a denominator, the number on the bottom.

Fractions are still used commonly in everyday language, ½ a cup of sugar, 2/3 of the class, ¼ tank of gas and so on. Fractions are not used as commonly in business settings or in mathematics because of the difficulty in working with fractions mathematically.

Denominator: The denominator refers to how many pieces it takes to make a whole, or one.

Numerator: The numerator is how many of the pieces identified by the denominator there are.

So, ¾ means it takes four of these pieces to make a whole and you have 3 of the four.

Fractions become somewhat difficult for math purposes because there can be many different denominators. When using fractions in math calculations, you must often find a common denominator.

Adding fractions

To add two fractions, or mixed numbers containing fractions, the denominators must be the same. This means you must find a denominator that both fractions can use and then convert either or both fractions to a new fraction using the same denominator.

Once the fractions have a common denominator (or already had one to begin with), to add fractions, simply add the numerators, keeping the denominator the same.

To find a common denominator, you need to find a value that both numbers are divisible by. Let’s look at this example:

We want to add ¼ + ½

1. First, you need to find the least common denominator

The least common denominator is the smallest number that both denominators can be represented as. You find this value by listing the multiples of each denominator until you find the smallest they can share.

Multiples of 2 are 2, 4, 6, 8, 10, 12, 15, 16, and so on.

Multiples of 4 are 4, 8, 12, 16 and so on.

The smallest (least) common denominator is 4.

1 / 4 already has 4 as a denominator, so do nothing to it.

Multiplying both the numerator and denominator by 2 will turn

1 / 2 into 2 / 4

Now both fractions have a common denominator of 4.

2. Next, add the numerators to solve the equation.

1/4+ 1/2= 1/4+ 2/4= 3/4

Subtracting fractions

To subtract fractions, the fractions must also have a common denominator. Once you find this and convert each fraction to a common denominator, you can simply subtract the numerators.

Multiplying Fractions

To multiply fractions, you multiply the numerators and the denominators. For example:

Dividing Fractions

To divide fractions, invert the divisor and then multiply.

Sponsored Ads

---